Simulation-based inference: confidence intervals

1 / 30

Big picture

2 / 30

Terminology

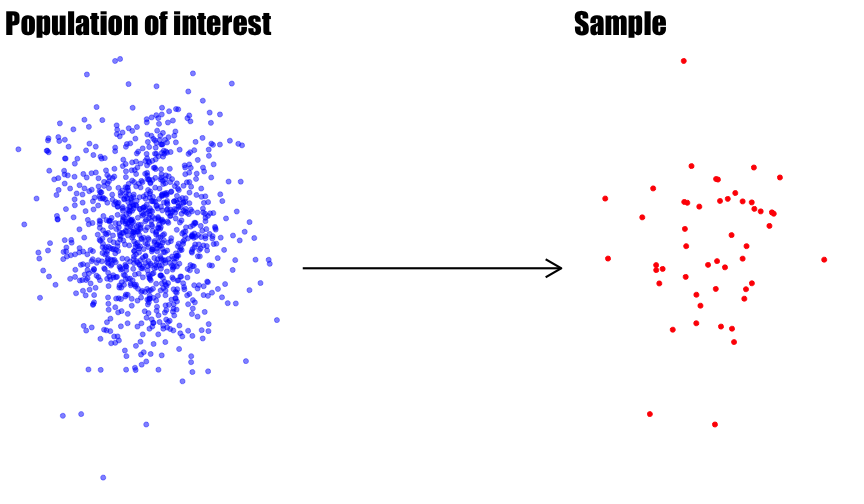
Population: a group of individuals or objects we are interested in studying

Parameter: a numerical quantity derived from the population (almost always unknown)

Sample: a subset of our population of interest

Statistic: a numerical quantity derived from a sample

Quantity	Parameter	Statistic
Mean	$μ$	$\bar{x}$
Variance	$σ^{2}$	$s^{2}$
Standard deviation	$σ$	$s$
Median	$M$	$\tilde{x}$
Proportion	$p$	$\hat{p}$

3 / 30

Statistical inference

Statistical inference is the process of using sample data to make conclusions about the underlying population the sample came from.

Estimation: estimating an unknown parameter based on values from the sample at hand
Testing: evaluating whether our observed sample provides evidence for or against some claim about the population

Today we will focus on estimation.

4 / 30

Estimation

5 / 30

Point estimate

A point estimate is a single value computed from the sample data to serve as the "best guess", or estimate, for the population parameter.

6 / 30

Point estimate

A point estimate is a single value computed from the sample data to serve as the "best guess", or estimate, for the population parameter.

Suppose we were interested in the population mean. What would be natural point estimate to use?

6 / 30

Point estimate

A point estimate is a single value computed from the sample data to serve as the "best guess", or estimate, for the population parameter.

Suppose we were interested in the population mean. What would be natural point estimate to use?

Quantity	Parameter	Statistic
Mean	$μ$	$\bar{x}$
Variance	$σ^{2}$	$s^{2}$
Standard deviation	$σ$	$s$
Median	$M$	$\tilde{x}$
Proportion	$p$	$\hat{p}$

6 / 30

Point estimate

A point estimate is a single value computed from the sample data to serve as the "best guess", or estimate, for the population parameter.

Suppose we were interested in the population mean. What would be natural point estimate to use?

Quantity	Parameter	Statistic
Mean	$μ$	$\bar{x}$
Variance	$σ^{2}$	$s^{2}$
Standard deviation	$σ$	$s$
Median	$M$	$\tilde{x}$
Proportion	$p$	$\hat{p}$

What is the downside to using point estimates?

6 / 30

Confidence intervals

A plausible range of values for the population parameter is an interval estimate. One type of interval estimate is known as a confidence interval.

7 / 30

Confidence intervals

A plausible range of values for the population parameter is an interval estimate. One type of interval estimate is known as a confidence interval.

spear

net

If we report a point estimate, we probably won’t hit the exact population parameter.
If we report a range of plausible values, we have a good shot at capturing the parameter.

7 / 30

Variability of sample statistics

In order to construct a confidence interval we need to quantify the variability of our sample statistic.
For example, if we want to construct a confidence interval for a population mean, we need to come up with a plausible range of values around our observed sample mean.
This range will depend on how precise and how accurate our sample mean is as an estimate of the population mean.
Quantifying this requires a measurement of how much we would expect the sample mean to vary from sample to sample.

8 / 30

Variability of sample statistics

In order to construct a confidence interval we need to quantify the variability of our sample statistic.
For example, if we want to construct a confidence interval for a population mean, we need to come up with a plausible range of values around our observed sample mean.
This range will depend on how precise and how accurate our sample mean is as an estimate of the population mean.
Quantifying this requires a measurement of how much we would expect the sample mean to vary from sample to sample.

Suppose you randomly sample 50 students and 5 of them are left handed. If you were to take another random sample of 50 students, how many would you expect to be left handed? Would you be surprised if only 3 of them were left handed? Would you be surprised if 40 of them were left handed?

8 / 30

Quantifying the variability of a sample statistic

We can quantify the variability of sample statistics using

simulation: via bootstrapping or resampling techniques (today);
theory: via Central Limit Theorem (later in the course).

9 / 30

Bootstrapping

10 / 30

Bootstrapping

The term bootstrapping comes from the phrase "pulling oneself up by one’s bootstraps", to help oneself without the aid of others.

In this case, we are estimating a population parameter, and we’ll accomplish it using data from only from the given sample.

This notion of saying something about a population parameter using only information from an observed sample is the crux of statistical inference, it is not limited to bootstrapping.

"The population is to the sample as the sample is to the bootstrap sample" – Fox, 2008

11 / 30

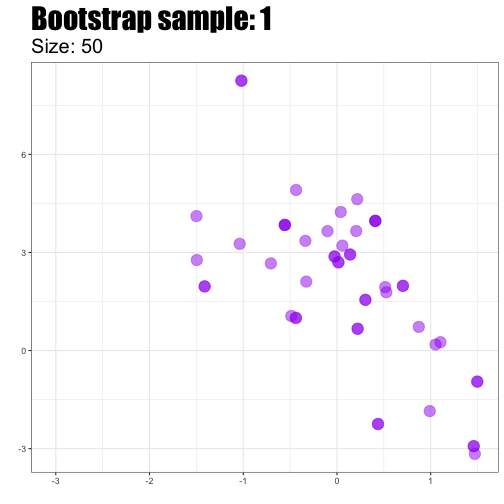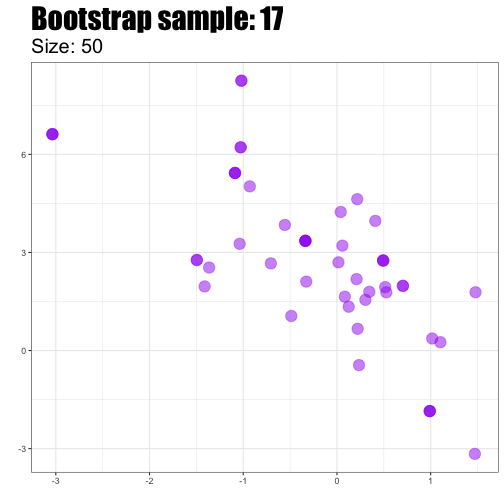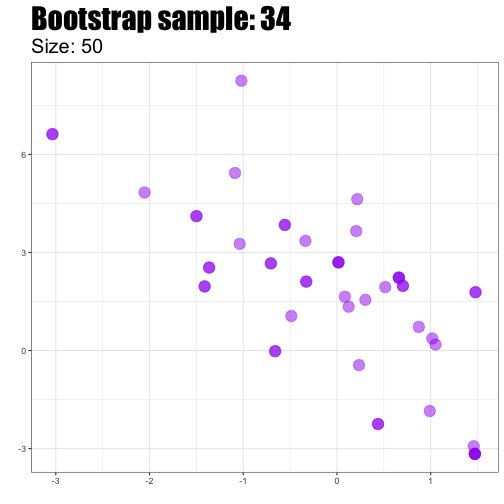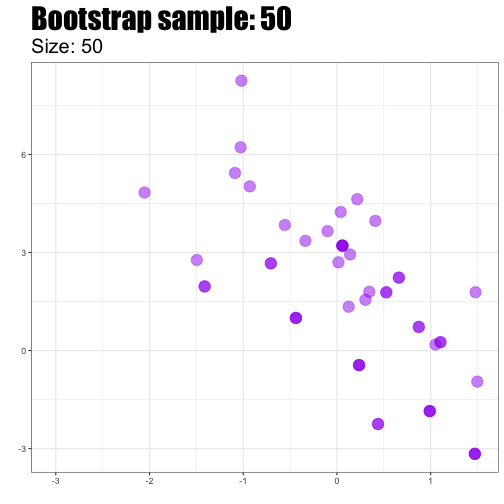
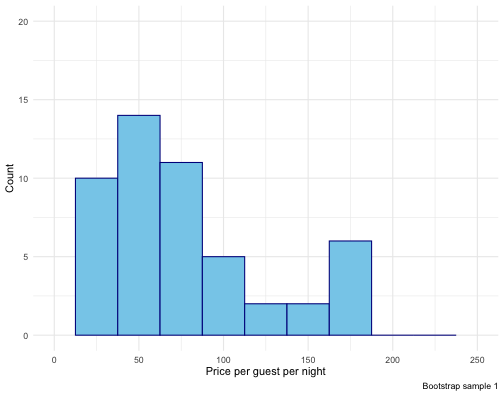
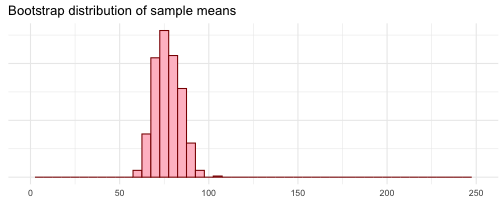
Bootstrapping scheme

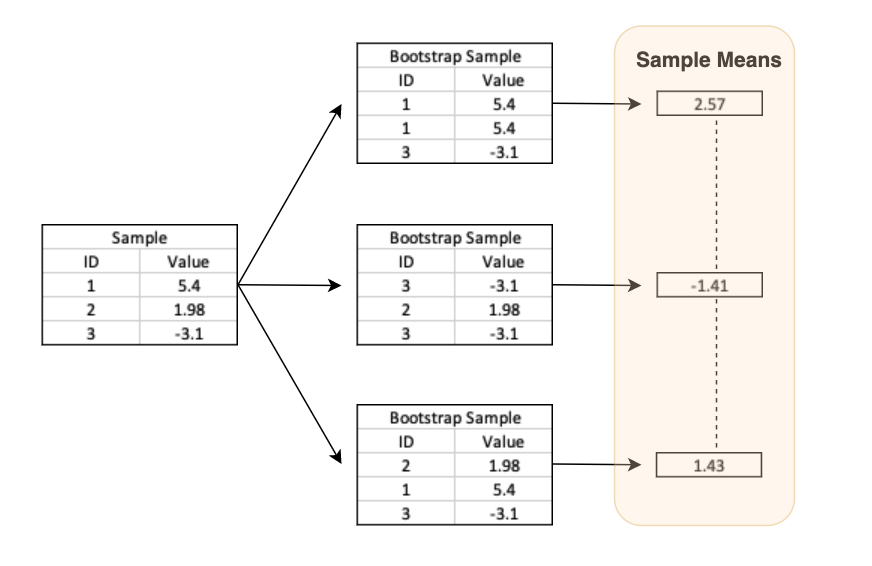
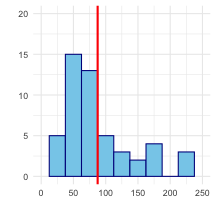
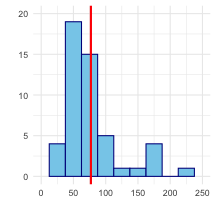
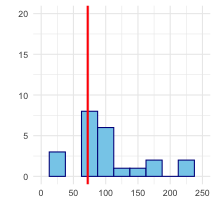
Take a bootstrap sample - a random sample taken with replacement from the original sample, of the same size as the original sample.
Calculate the bootstrap statistic - a statistic such as mean, median, proportion, slope, etc. computed from the bootstrap samples.
Repeat steps (1) and (2) many times to create a bootstrap distribution - a distribution of bootstrap statistics.
Calculate the bounds of the XX% confidence interval as the middle XX% of the bootstrap distribution.

12 / 30

Bootstrapping scheme (1 - 2) visualized

13 / 30

Bootstrapping scheme (1 - 2) animated

For each bootstrap sample, we would compute our statistic of interest, e.g. correlation.

14 / 30

Asheville Airbnb

How much should we expect to pay for an Airbnb in Asheville?

15 / 30

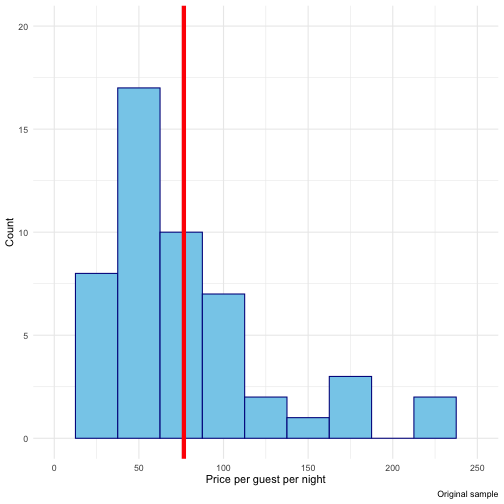
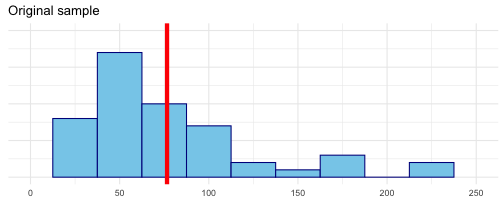
Asheville data

Inside Airbnb scraped all Airbnb listings in Asheville, NC, that were active on June 25, 2020.

Population of interest: listings in the Asheville with at least ten reviews.

Parameter of interest: Mean price per guest per night among these listings.

What is the mean price per guest per night among Airbnb rentals in June 2020, among Airbnbs with at least ten reviews in ZIP codes 28801 - 28806?

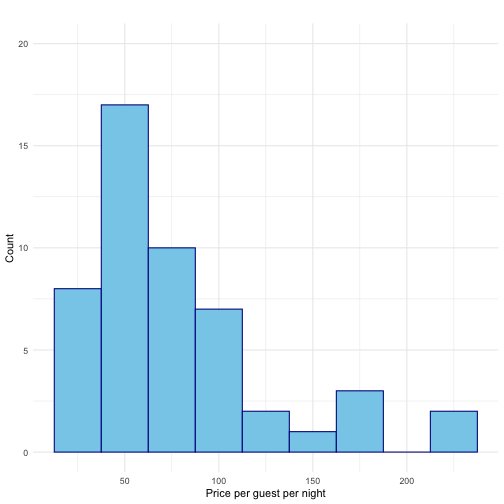
The dataset asheville.csv contains the price per guest (ppg) for a random sample of 50 listings.

16 / 30

Point estimate

A point estimate is a single value computed from the sample data to serve as the "best guess", or estimate, for the population parameter. Let's use the sample mean from our dataset in order to do so.

library(tidyverse)
abb <- read_csv("data/asheville.csv")
abb %>% 
  summarize(mean_price = mean(ppg))

#> # A tibble: 1 x 1
#>   mean_price
#>        <dbl>
#> 1       76.6

Is this enough? Are we done? Is there any more insight that can be gained?

17 / 30

Visualizing our sample

18 / 30

The original sample

19 / 30

Step-by-step

Step 1. Take a bootstrap sample: a random sample taken with replacement from the original sample, of the same size as the original sample:

20 / 30

Step-by-step

Step 1. Take a bootstrap sample: a random sample taken with replacement from the original sample, of the same size as the original sample:

20 / 30

Step-by-step

Step 2. Calculate the bootstrap statistic (in this case, the sample mean) using the bootstrap sample:

21 / 30

Step-by-step

Step 2. Calculate the bootstrap statistic (in this case, the sample mean) using the bootstrap sample:

21 / 30

Step-by-step

Step 3. Do steps 1 and 2 over and over again to create a bootstrap distribution of sample means:

22 / 30

Step-by-step

Step 3. Do steps 1 and 2 over and over again to create a bootstrap distribution of sample means:

22 / 30

Step-by-step

Step 3. In this plot, we've taken 500 bootstrap samples, calculated the sample mean for each, and plotted them in a histogram:

23 / 30

Step-by-step

Step 3. Here we compare the bootstrap distribution of sample means to that of the original data. What do you notice?

24 / 30

Step-by-step

Step 4. Calculate the bounds of the bootstrap interval by using percentiles of the bootstrap distribution

25 / 30

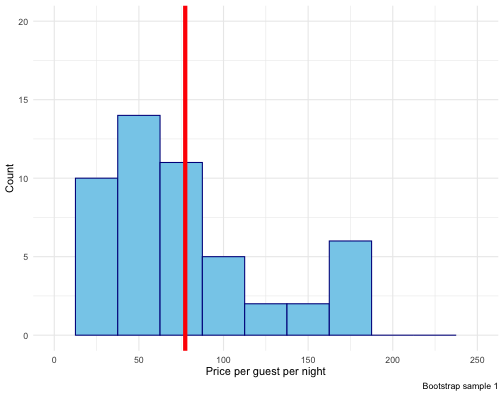
CI interpretation

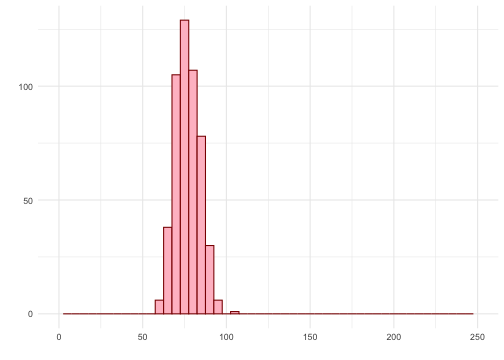
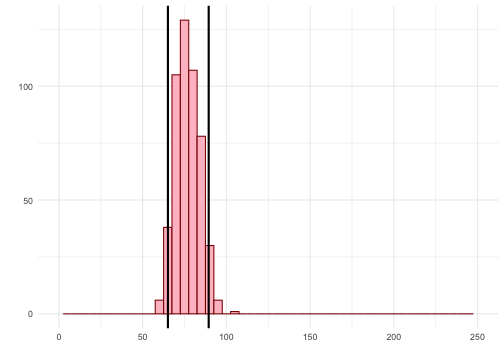
Using the 2.5th and 97.5th quantiles as bounds for our confidence interval gives us the middle 95% of the bootstrap means. Our 95% CI is (65.1, 89.4).

Does this mean there is a 95% chance that the true mean price per night in the population is contained in the interval (65.1, 89.4)?

26 / 30

NO

27 / 30

Interpreting a confidence interval

The population parameter is either in our interval or it isn't. It can't have a "95% chance" of being in any specific interval.

The bootstrap distribution captures the variability of the sample mean, but is based on our original sample. If we obtained a different sample to begin with, (perhaps centered somewhere else), then maybe our estimated 95% confidence interval would have been different also.

28 / 30

Interpreting a confidence interval

The population parameter is either in our interval or it isn't. It can't have a "95% chance" of being in any specific interval.

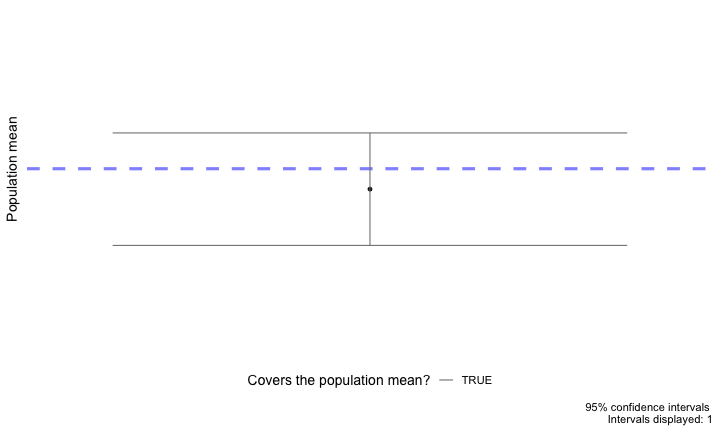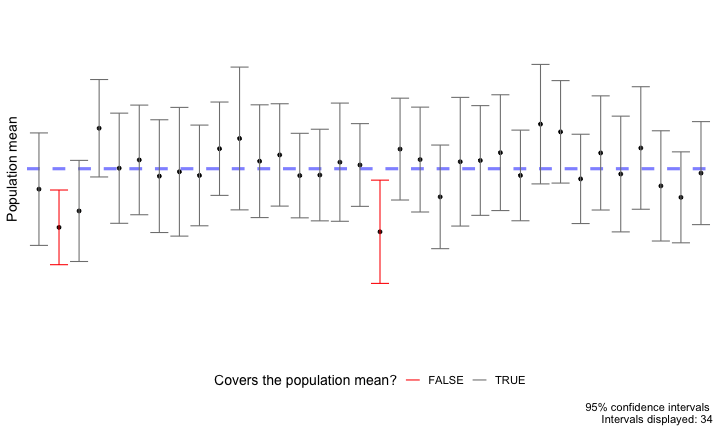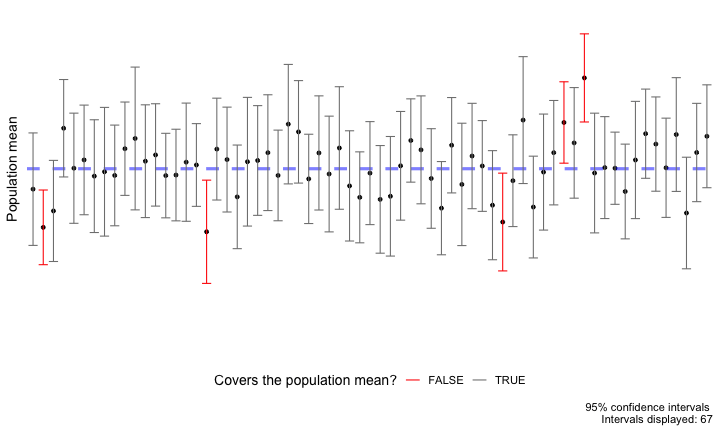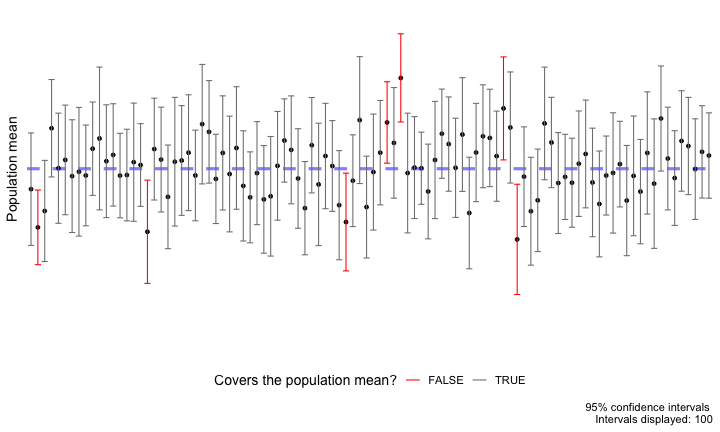
All we can say is that, if we were to independently take repeated samples from this population and calculate a 95% CI for the mean in the exact same way, then we would expect 95% of these intervals to truly cover the population mean. However, we never know if any particular interval(s) actually do!

This is the meaning of statistical confidence.

Warning: Be careful with the concepts of repeatedly re-sampling from the sample to obtain a bootstrap distribution vs. taking a new sample entirely.

28 / 30

Interpretation visualization

29 / 30

Click the link below to create the repository for lecture notes #13.

https://classroom.github.com/a/OHpXIUaw

30 / 30

Help

Keyboard shortcuts

↑, ←, Pg Up, k

Go to previous slide

↓, →, Pg Dn, Space, j

Go to next slide

Home

Go to first slide

End

Go to last slide

Number + Return

Go to specific slide

b / m / f

Toggle blackout / mirrored / fullscreen mode

Clone slideshow

Toggle presenter mode

Restart the presentation timer

?, h

Toggle this help